Alberto Bagnai
Università Gabriele d’Annunzio
Centre for Globalisation Research – Queen Mary University
CREAM – Université de Rouen
a/simmetrie
Christian Alexander Mongeau-Ospina
a/simmetrie
Introduzione
Questa nota riporta i risultati preliminari di uno studio condotto da Alberto Bagnai e Christian Alexander Mongeau Ospina nel quadro dell’attività di ricerca promossa da a/simmetrie, presentati nel convegno internazionale “Un’Europa senza euro” promosso da a/simmetrie col Manifesto di Solidarietà Europea.
Utilizzando un campione di 228 osservazioni mensili dal gennaio 1994 al dicembre 2012 è stato stimato l’impatto del costo del barile e del tasso di cambio (costo della valuta estera) sul prezzo industriale della benzina (prima delle accise e dell’IVA). Il prezzo alla pompa è stato poi calcolato sommando le accise e calcolando l’IVA. Lo scopo dello studio è quello di valutare quale sarebbe l’impatto sul prezzo alla pompa di una svalutazione del cambio della valuta nazionale di un ordine comparabile a quello atteso in caso di uscita dall’euro, stimato in una forchetta fra il 20% e il 40% (si veda ad esempio la Tab. 6 dello studio di Roger Bootle Leaving the euro: a practical guide).
La conclusione principale dello studio è che anche nel caso estremamente improbabile di una svalutazione immediata del 40% (da un mese al successivo), una modesta manovra compensativa delle accise sarebbe sufficiente a contenere l’aumento del prezzo alla pompa attorno al 6% (dopo un iniziale picco attorno al 10%).
I dati
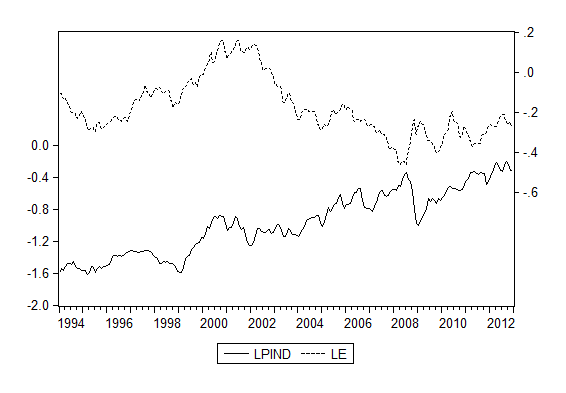
I dati su prezzo della benzina, accise e IVA provengono dall’Oil bulletin dell’Osservatorio della Commissione Europea sul mercato dell’energia. Quelli sul tasso di cambio fra euro e dollaro e sul costo del barile in dollari provengono dalle International Financial Statistics del Fondo Monetario Internazionale. Prima del 1999 abbiamo utilizzato il tasso di cambio Ecu/dollaro. Il costo del barile è quello medio fra Dubai Fateh, Western Texas Intermediate, e Brent (variabile Average crude price). Il loro andamento è rappresentato nelle due figure seguenti, dove LPIND è il prezzo industriale della benzina, LE il tasso di cambio (costo di un dollaro in euro), LP il prezzo del barile in dollari, e tutte le variabili sono logaritmizzate.
Relazione di lungo periodo
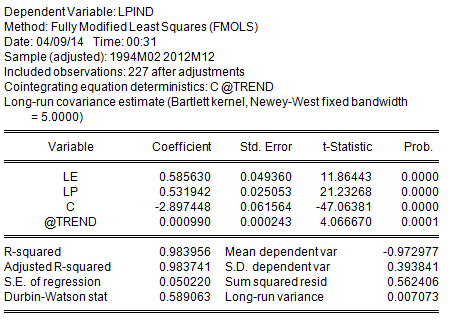
Le tre variabili sono legate da una relazione statistica estremamente robusta. Le elasticità di lungo periodo sono state stimate utilizzando lo stimatore Fully Modified Ordinary Least Squares di Phillips e Hansen. Il prezzo industriale ha un’elasticità di 0.58 al tasso di cambio e di 0.53 al prezzo del barile. Questo significa che solo il 58% di una variazione percentuale del cambio viene traslato sul prezzo industriale della benzina.
I test di cointegrazione respingono la nulla di assenza di cointegrazione fra le variabili (dettagli nella versione finale dell’articolo).
Il modello dinamico
Le tre variabili sono legate da una
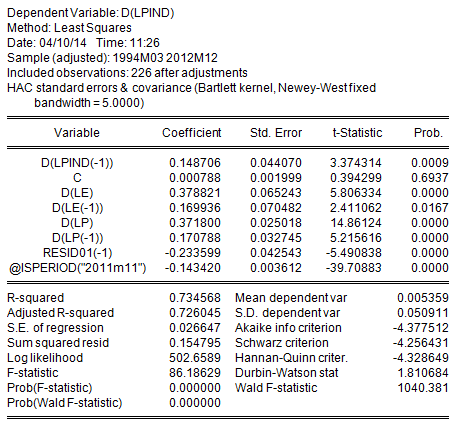
relazione dinamica di tipo “a correzione dell’errore” (Engle e Granger, 1987) particolarmente robusta in termini statistici.
RESID01 è il residuo cointegrante, che entra con una t superiore a 5 in valore assoluto, indicando una forte cointegrazione fra le variabili. Il modello spiega il 73% della variabilità della variazione mensile del prezzo della benzina. Si tratta di una percentuale decisamente alta per un modello su dati campionati con questa frequenza, il che lascia supporre che esso sia relativamente affidabile in termini previsionali.
La bontà della previsione
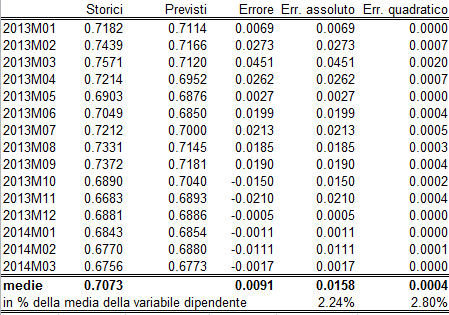
Prima di utilizzare il modello per analisi di scenario, lo abbiamo testato in previsione sul periodo dal gennaio 2013 al marzo 2014 (15 mesi). I risultati della previsione dinamica in queste 15 osservazioni fuori dal campione sono riassunti in questa tabella:
L’errore medio assoluto è pari a 1.58 centesimi, cioè al 2.24% della variabile dipendente, mentre la radice dell’errore quadratico medio è pari al 2.80% della variabile dipendente.
Partendo da questa previsione del prezzo industriale abbiamo ottenuto quella del prezzo alla pompa con la relazione:
BENZINA = (PIND +ACCISA) x (1 + IVA)
dove BENZINA è il prezzo alla pompa, ACCISA l’ammontare delle accise, e IVA l’aliquota IVA. La previsione del prezzo alla pompa è ancora più accurata:
Lo scenario di riferimento
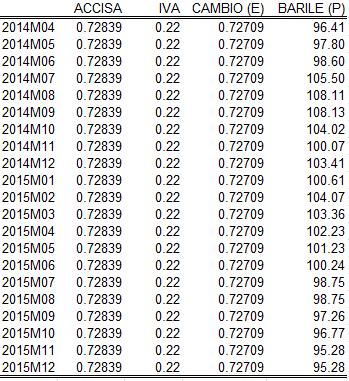
Per simulare l’impatto di una svalutazione del cambio sul prezzo della benzina abbiamo prima costruito uno scenario di riferimento estrapolando la variabile dipendente sul periodo dal maggio del 2014 al dicembre del 2015 facendo le seguenti ipotesi sulle quattro variabili esogene del modello (l’importo delle accise, l’aliquota IVA, il tasso di cambio e il prezzo del barile):
In sostanza, si ipotizza che le variabili fiscali rimangano costanti ai livelli attuali, e la stessa ipotesi viene fatta per il tasso di cambio, mentre per il prezzo del barile si usano le previsioni emesse dalla U.S. Energy Information Administration. La previsione ottenuta sotto queste ipotesi è riportata nel grafico seguente:
Il prezzo alla pompa evolve seguendo l’evoluzione prevista del prezzo del petrolio. Si noti che questa previsione non va intesa come una effettiva previsione del prezzo della benzina, che richiederebbe di prevedere anche l’andamento del tasso di cambio. Dato che il livello attuale del cambio dell’euro è fortemente sopravvalutato, è molto probabile che il prezzo futuro della benzina sia più alto di quello previsto sotto le ipotesi dello scenario neutro. Questo però è irrilevante ai fini della nostra analisi, perché quello che qui interessa non è tanto determinare quanto sarà il prezzo in futuro, ma quanto potrebbe variare rispetto allo s
cenario “neutro” rappresentato qui sopra nell’ipotesi che il cambio ceda in una misura compresa fra il 20% e il 40% (intese come svalutazione minima e massima che è lecito attendersi alla luce degli studi citati).
L’impatto di una svalutazione secca del 20%
Lo studio considera una molteplicità di scenari. Qui ne riportiamo due. Il primo considera l’ipotesi di una svalutazione “secca”, da un mese all’altro, pari al 20% del cambio euro/dollaro (più precisamente, dato che utilizziamo la quotazione incerto per certo, ipotizziamo che aumenti del 20% il prezzo in euro di un dollaro). L’impatto di una simile svalutazione sul prezzo alla pompa è riportato in questa figura:
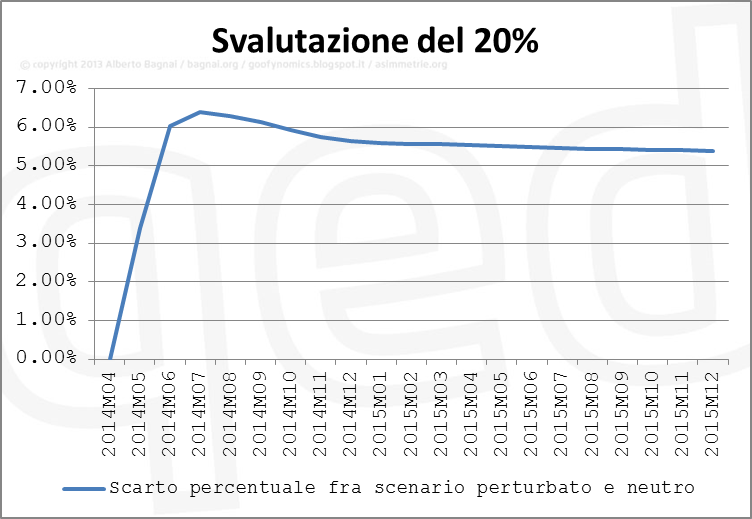
In sintesi, il prezzo della benzina aumenterebbe abbastanza rapidamente, portandosi circa 10 centesimi al di sopra dello scenario neutro (Baseline), per poi diminuire lievemente. Il grafico successivo riporta lo scarto fra lo scenario “perturbato” (Scenario1, svalutazione del 20%) e lo scenario neutro (baseline):
Lo scarto percentuale si attesta fra il 5% e il 6%. Questo risultato è prevedibile, perché dato che il prezzo industriale risponde per il 58% a una variazione del cambio, e che il prezzo alla pompa è composto per metà di accise, l’impatto di una svalutazione del 20% del cambio sul prezzo alla pompa è di circa 0.2×0.58×0.5=5.8%.
L’impatto di una svalutazione secca del 40% compensata da una riduzione graduale delle accise
In questo secondo scenario consideriamo gli effetti di una svalutazione di entità doppia della precedente (il costo del dollaro aumenta del 40%, anziché del 20%), ma ipotizziamo anche che il suo impatto sui prezzi venga contrastato dal governo riducendo gradualmente le accise. La riduzione ipotizzata è molto contenuta: un centesimo al mese per sei mesi, fino a un massimo di sei centesimi. La perdita di gettito per il primo anno è stimata intorno fra i 300 e i 400 milioni di euro, nell’ipotesi però che la svalutazione non determini una ripresa dell’attività economica e quindi dei consumi (nel qual caso la riduzione dell’accisa sarebbe almeno parzialmente compensata da un aumento delle vendite di benzina).
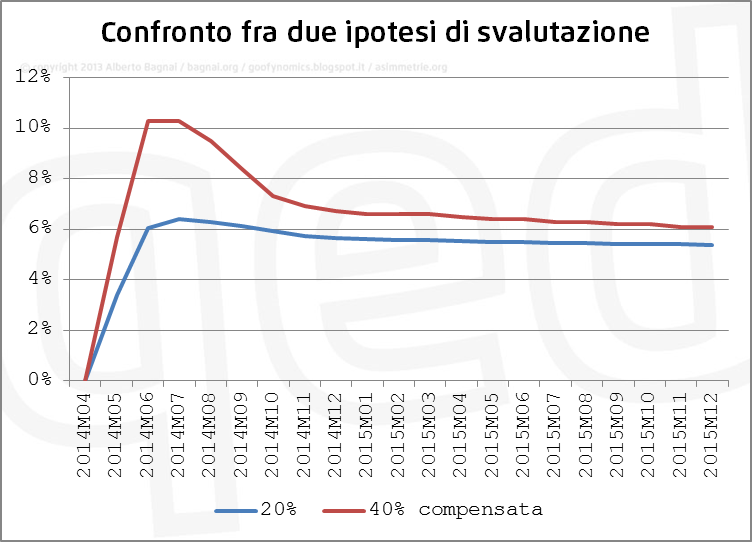
La figura seguente riporta gli scarti dallo scenario neutro dei due scenari “perturbati”: quello di svalutazione del 20%, e quello di svalutazione del 40% “compensata”, espressi come aumento percentuale degli scenari perturbati rispetto quello neutro:
Nel caso di svalutazione del 40% il prezzo della benzina aumenterebbe abbastanza rapidamente del 10% (circa 18 centesimi al litro). La graduale manovra compensatoria delle accise però riporterebbe l’aumento intorno al 7% nel lungo periodo (una misura non dissimile da quanto si avrebbe nel caso di svalutazione del 20%).
Possiamo anche osservare gli stessi risultati come scarti assoluti, anziché percentuali, dallo scenario neutro, cioè come effettivo aumento del prezzo in euro determinato dalla svalutazione:
In entrambi i casi l’impatto di lungo periodo sarebbe vicino ai 10 centesimi in più al litro. Può essere utile ricordare che le
manovre di austerità dei precedenti governi hanno determinato aumenti ben maggiori attraverso la manovra delle accise.
Naturalmente queste simulazioni sono di equilibrio parziale, e non tengono conto, quindi, di effetti successivi, come ad esempio l’aumento del prezzo industriale determinato da altri fattori (quali la spinta inflazionistica causata dalla svalutazione del cambio). Nella versione definitiva del lavoro, della quale qui si forniscono solo i risultati principali, si mostra che questi effetti, alla luce delle esperienze storiche, sono verosimilmente di ampiezza trascurabile. L’idea che una svalutazione del 40% porterebbe il prezzo della benzina a €2.40 (la cosiddetta ipotesi del “fare il pieno con la carriola di monetine”) sembra quindi smentita dalle evidenze statistiche. Questo risultato si conforma a quelli di una vasta letteratura scientifica la quale conferma che la traslazione di una variazione del cambio sui prezzi finali generalmente è piuttosto contenuta, almeno nelle economie occidentali (Goldfajn e Werlang, 2000).
Riferimenti
Engle, Robert F & Granger, Clive W J, 1987. “Co-integration and Error Correction: Representation, Estimation, and Testing,” Econometrica, Econometric Society, vol. 55(2), pages 251-76, March.
Goldfajn, Ilan & Sergio R.C. Werlang, 2000. “The pass-through from depreciation to inflation : a panel study,” Textos para discussão 423, Department of Economics PUC-Rio (Brazil).
Phillips, Peter C B & Hansen, Bruce E, 1990. “Statistical Inference in Instrumental Variables Regression with I(1) Processes,” Review of Economic Studies, Wiley Blackwell, vol. 57(1), pages 99-125, January.